有很多次为了讲解我之前关于土动力学的研究工作,讲到连续介质的平衡方程及求解,听者闻之呆立半晌,想毕是在消化知识点,或者这个知识点有点消化不良。为此开篇用本文来促进知识消化,形成线性连续介质力学推导思维。
1.位移表示的平衡方程的搭建
首先要介绍几个耳熟能详但又不知为何物的概念,什么是微元体,什么是平衡方程、几何方程,什么是本构关系。先讲微元体,为什么要从物体内部挖一块出来分析呢?
我们都知道外力会导致弹性体内部发生变形,在连续介质范畴内,这一变形是空间连续的。为了得到物体的变形描述,我们可以给物体内部标记无数个点,想要多少就标多少,然后声明这些点的空间位置,三维空间里我们用坐标\((X_1, X_2, X_3)\)来表示,这儿不限定为直角坐标\((x, y, z)\)或柱坐标\((r, \theta, z)\)等,甚至不限定为正交坐标系,如此一来弹性体的变形最后归结为获得在外力作用下每个标记点的相对位置变化,这一大堆的相对位置变化数据,就称为位移场,因为这些数据是与空间坐标相关的变量。
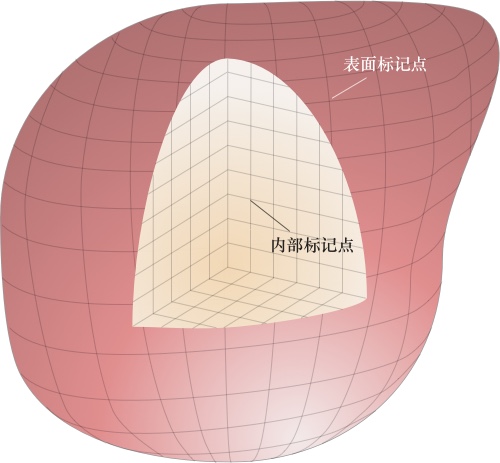
图1. 弹性体表面和内部标记点示意,图中的标记点数量不多,如果为得到更精确的连续体变形场量,需要设置更多的标记点
但是标记点的量如此大,比如有十万个标记点,我们难道要把全部的标记点位置都得到吗?这就是而对于物体内部标记点也就是说这就给我们一个力学思维启示:如果单独抽离一小块体,把物体受到的“内力”假想为块体表面受到的外力,能否得到它的变形特征呢?这时微元体的概念就浮现了,从弹性体中任意位置——注意是任意位置——沿三维轴线方向上切取一个小块都可以算做
微元体,其边长分别为\(\text d x_1\)、\(\text d x_2\)、\(\text d x_3\),接下来将以局部代替整体,对它进行受力分析。
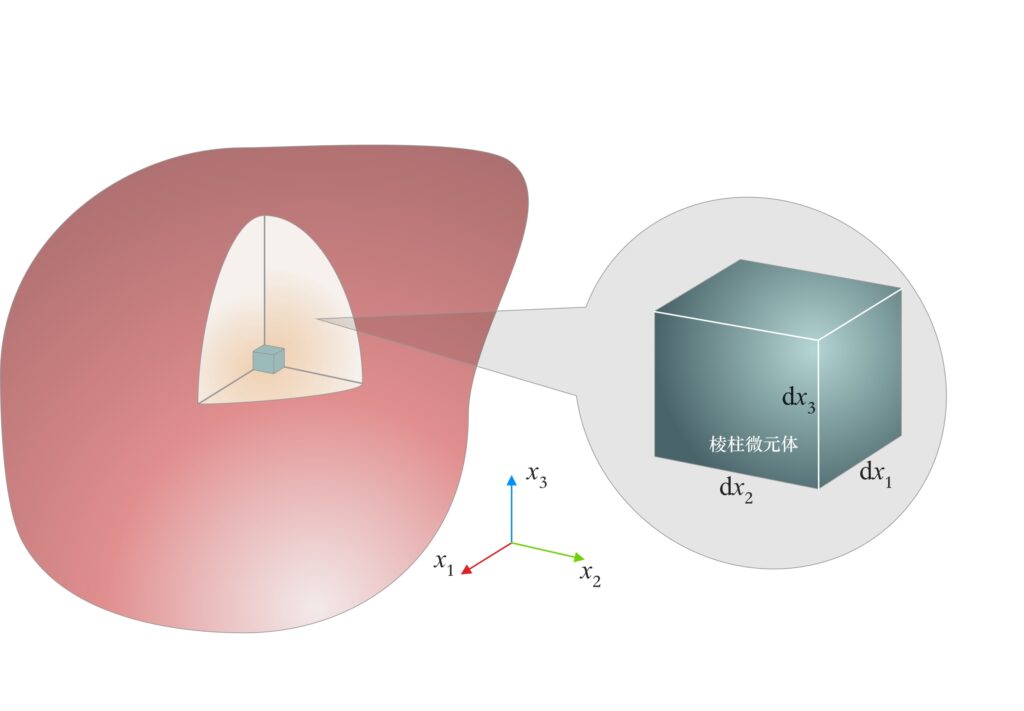
图2. 弹性体内部任意位置处沿\(x_1\)、\(x_2\)、\(x_3\)三个轴线方向挖出的微元体
现在我们知道微元体位置处的内力可以处理成它表面的一组外力,建立一组力的平衡方程组,在三维空间那就是三个坐标方向上的平衡方程。修读过弹性力学或者材料力学的读者都知道,任何物体表面受到的应力都可以分解成两种,一种是与受力表面垂直的法向正应力\(\sigma\),另一种是与受力面平行的切向应力\(\tau\)。在连续介质力学范畴中,这两种力其实是同一类型的力,都可以用\(\sigma_{ij}\)来表示,其中下标\(i, j\)指的是面的法向方向和力的指向方向,并规定
法向为正的表面上指向正方向(法向为负的表面上指向负方向)的应力为正,反之为负。考虑到微元体的长度分别为\(\text d x_1\)、\(\text d x_2\)和\(\text d x_3\),根据连续函数的一阶泰勒展开可得微元体六个面的受力情况,如下图:

图3. 微元体六个面的全部应力示意图
以方向1的受力平衡为例(图中红色箭头部分),根据牛顿第二定律可得到微元体
平衡方程
\[\frac{\partial \sigma_{11}}{\partial x_1}\text d x_1\cdot\text d x_2 \text d x_3+\frac{\partial \sigma_{21}}{\partial x_2}\text d x_2\cdot\text d x_3\text d x_1+\frac{\partial \sigma_{31}}{\partial x_3}\text d x_3\cdot\text d x_1 \text d x_2=\rho \cdot\text d x_1\cdot \text d x_2\cdot \text d x_3 \frac{\partial^2 u_1}{\partial t^2}\]
约去通项,再用张量的形式(如果不懂张量得另外补课了)来表示这组方程组,就得到
\[\sigma_{ij,i}=\rho\cdot \ddot{u}_j\]
是不是超级简洁(完全看不懂好吗)?但是这个方程仍然不完美,方程右边是位移\(u_i\),左边是应力\(\sigma_{ij,i}\),显然两侧是不能化简操作的,怎么办呢?别急,祭出我们第二个法宝——
本构关系。以最简单的满足Hooke本构法则的材料为例(就是那位初中物理中教你弹簧的力等于一个常数乘以伸长量\(f=k\cdot x\)的那位),应力\(\sigma_{ij}\)可以表示为应变\(\epsilon_{ij}\)的函数
\[\sigma_{ij}=\lambda \epsilon_{kk}\delta_{ij}+2\mu\cdot\epsilon_{ij}\]
其中\(\lambda\)和\(\mu\)为lame常数,\(\mu\)是材料的剪切模量,我们应该非常熟悉了,\(\delta_{ij}\)为kronecker delta算子。这个方程就很有效地把应力转换为应变表达,两者用模量的概念联系起来(多少学者穷其一生就是追求各种本构关系中的各种模量的计算方法、试验方法)。现在还不着急把这个式子代入到平衡方程,还差一步,还记得我们开始做了很多标记点吗,这些孤立的点的运动只能用位移这个向量来表示,接下来就是要把位移推出来的时候了,祭出
几何方程。应变其本质用一句话概括,就是长度或角度的改变量占原有长度或角度的比例,当这个变形很大,计算起来就很复杂了,一般是用泰勒级数形式来表示,但如果变形很小就比较简单了,因为泰勒级数高阶项都可以近似为0了。以小变形为例,应变\(\epsilon_{ij}\)表示成位移的一阶展开函数如下
\[\epsilon_{ij}=\frac{1}{2}(u_{i,j}+u_{j,i})\]
发现了吗,应变\(\epsilon_{ij}\)原来也可以由位移\(u_i\)表示,任务就快完成了。我们把这个式子代入本构关系,再进一步代入平衡方程,得到变形后的平衡方程
\[[\lambda u_{k,k}\delta_{ij}+\mu\cdot(u_{i,j}+u_{j,i})]_{,i}=(\lambda +\mu)u_{i,ij}+\mu u_{j,ii}=\rho\cdot \ddot{u}_j\]
这儿的推导用到了很多关于张量的哑标、\(\delta_{ij}\)对下标替换的规则,请自行补课,总之推导思路就是从位移到应变再到应力(\(u_i \rightarrow \epsilon_{ij}\rightarrow\sigma_{ij}\)),导入到平衡方程中建立只含位移的方程,就宣告结束了。惊喜不惊喜?呵呵,你高兴得太早了!
2. 位移表示的平衡方程的解耦
观察上式我们可以看到,虽然因变量只有位移,但几个位移是相互地交织出现在同一个公式中(耦合),要想办法把它们解开(解耦)。这儿我们推荐常用的势函数解答,假定位移向量可表示为一个标量势函数\(\phi\)和一个矢量势函数\(\psi_i\)的微分算子的形式,即
\[u_i=\phi_{,i}+\epsilon_{ijk}\psi_{k,j}\]
其中\(\epsilon_{ijk}\)为permutation symbol (Levi-Civita symbol),当\(ijk\)三个数字为1、2、3顺次次序时为1,比如“123”、“231”、“312”,反之则为\(-1\)。如此,代入到平衡方程得到
\[(\lambda +\mu)(\phi_{,i}+\epsilon_{ijk}\psi_{k,j})_{,ij}+\mu (\phi_{,j}+\epsilon_{jmn}\psi_{n,m})_{,ii}=\rho\cdot (\ddot\phi_{,j}+\epsilon_{jmn}\ddot\psi_{n,m})\]
拆解微分算子得
\[(\lambda +\mu)(\phi_{,iij}+\epsilon_{imn}\psi_{n,mij})+\mu (\phi_{,jii}+\epsilon_{jmn}\psi_{n,mii})=\rho\cdot (\ddot\phi_{,j}+\epsilon_{jmn}\ddot\psi_{n,m})\]
进一步化简,考虑到\(\epsilon_{ijk}\)下标对调正负号变换一次,\(\epsilon_{imn}\psi_{n,mij}=0\),则上式拆解成
\[\left[(\lambda +2\mu)\phi_{,ii}-\rho\cdot \ddot\phi\right]_{,j}+ \epsilon_{jmn}\left[\mu\psi_{n,ii}-\rho\cdot\ddot\psi_{n}\right]_{,m}=0\]
对比该方程左右两侧(更严谨的办法是分别乘以散度算子\(\nabla\cdot\)和旋度算子\(\nabla\times\),此处简化),方程要成立则必须同时满足
\[(\lambda +2\mu)\phi_{,ii}-\rho\cdot \ddot\phi=0, \qquad \mu\psi_{n,ii}-\rho\cdot\ddot\psi_{n}=0\]
或者
\[\phi_{,ii}-v_p^{-2}\ddot\phi=0, \qquad \psi_{n,ii}-v_s^{-2}\ddot\psi_{n}=0\]
其中,\(v_p=\sqrt{(\lambda +2\mu)/\rho}\)为P波波速,\(v_s=\sqrt{\mu/\rho}\)为S波波速。为何地震来临时,体波P波总是比S波要早来,因为它的速度公式就比S波大了将近一倍。这时候你应该问一个这样的问题:为什么推导到此,出现了波速一说呢,咱一开始不是冲着弹性体的平衡方程来的吗?这个问题我们后面找机会作文讨论吧。至此,弹性体的平衡关系给大致整明白了,工作量完成了一半。为什么说完成了一半,因为这两个函数的解答还有待提供一定数量的边界条件才能得到,下一篇文章我们就来讨论边界条件影响下的场论解答。暂时介绍这么多吧,希望读者阅完本篇会有所收获。
【版权声明】本文为作者原创内容,转载时必须标注文章的来源、文章链接、文章作者等基本信息,否则作者有权追究责任。根据《著作权法》相关规定,使用他人作品的,应当取得著作权人的许可。

文章评论
一楼踩一踩
@吃白饭舰长 谢谢舰长光顾船舱视察